학습개요
-Model of Secure System
-Theory of Secrecy Systems
· Condition for perfect secrecy
· Shannon Entropy
· Equivocation
· Perfect Secrecy
· Redundancy
· Unicity Distance
-Complexity Theory
Digital Signature Susceptibility
<MD5에서의 Hash값>
MD5:128비트 암호화 해시 함수
susceptibility: 민감성
Hash 동작 : m→ f(m)(=H(m))
m'≠m이면 f(m')≠f(m) 이어야한다.
m'≠m인데 f(m')=f(m)이면 attacker가 m'으로 f(m)에 접근할 수 있기때문에 보안이 취약해진다.
문제해결
① MD5를 더 많은 bit로 사용
② 동일한 hash를 가진 두 개의 사기성 문서를 발견하면 정보를 얻지 못하므로 해시함수의 결과값은 충분히 커야한다.
≫ 더 큰 hash를 사용하여 collision이 발생하지 않도록 해야한다.
≫ 더 많은 bit를 사용한다.
Model of Secure System
M → E(M,K) → C → D(C,K) → M
(이 때 secrecy를 위해 Key를 사용하며 secure channel을 통해 전달한다.)
Shannon Theory
secrecy problem은 noisy-channel problem과 유사하다.
redundancy: 그것이 없어도 전체 정보의 본질적인 뜻이 변하지 않는 정보. 즉, 필요없는 정보
Noisy Channel에서 redundancy를 통해 original message를 recover하듯, 해독 과정에서 암호화된 Cipher(Message+Noise)에서 Noise를 제거하여 M을 찾아내는 것이 서로 유사하다.
Priori and Posterior Probabilities
사전확률과 사후확률
사전확률 Pi로 모든 K 중에서 Ki를 선택하고, 사전확률 Qj로 모든 M 중에서 Mj를 선택하여 M은 Cipher text로 변환된다.
Cl=E(Mj,Ki)
attacker는 Cl만 볼 수 있으며 가능한 Mj와 Ki의 사후확률을 계산한다.
Condition for Perfect Secrecy
사후확률(posteriori probability)은 attacker의 knowlege를 나타낸다.
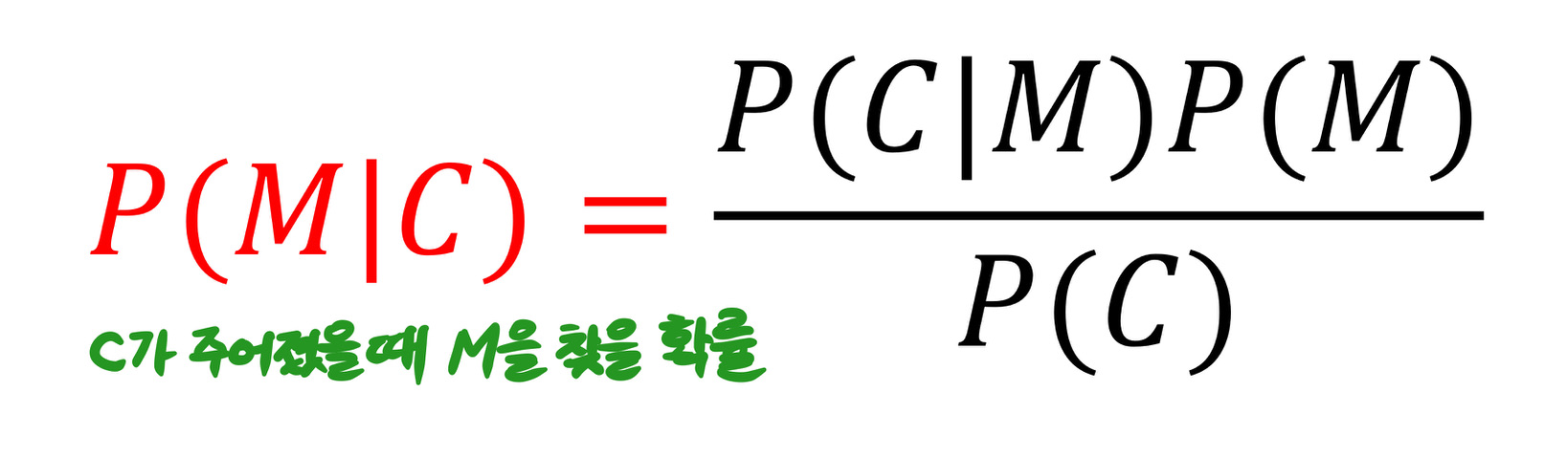
P(M|C) : C가 주어졌을 때 M을 찾을 확률
P(M|C)=P(M)이 되는 것이 가장 바람직하다. attacker가 C를 통해 아무정보도 얻지 못한다는 뜻이므로.
∴Perfect Secrecy를 위한 조건
① P(M|C) = P(M)
② P(C|M) = P(C)
perfect system이란 다수의 C와 M이 존재할 때 M을 C로 변환하는 적어도 하나의 key가 있는 상태를 말한다. attacker의 입장에서 guessing이 불가능하고 모두 같은 확률이 되도록 해야한다.
Shannon Entropy
Entropy: 불확실성
Shannon Entropy: random 변수의 예측 불가능성을 측정한 것.
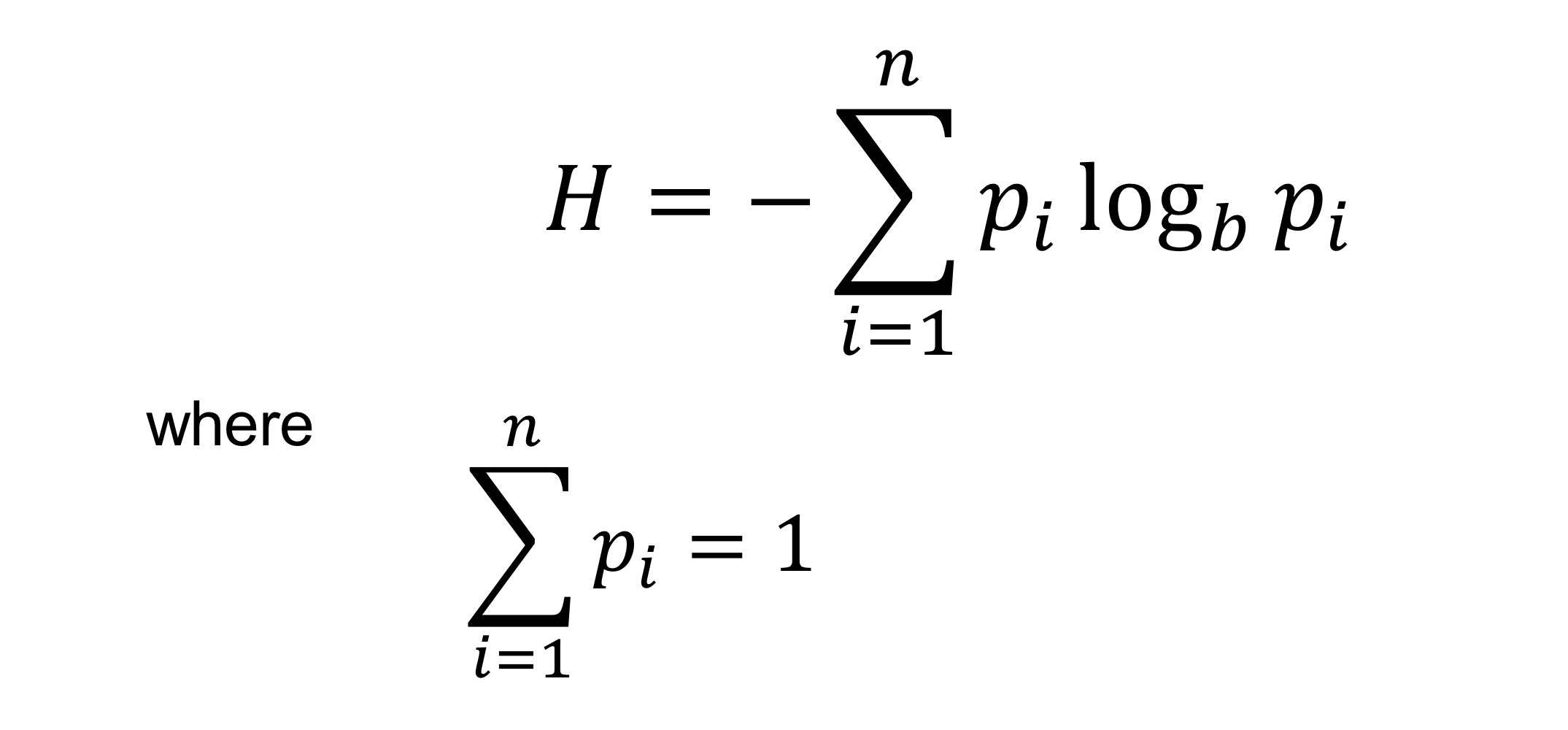
이 때, b는 bit의 경우 2, digit의 경우 10이 된다. 즉, 가능한 경우의 수이다.
예측이 어려울수록 불확실해지므로 Entropy가 크다고 한다. (Entropy가 클수록 좋음)
ex) 동전 던지기
H일 확률 : 1/2
T일 확률 : 1/2
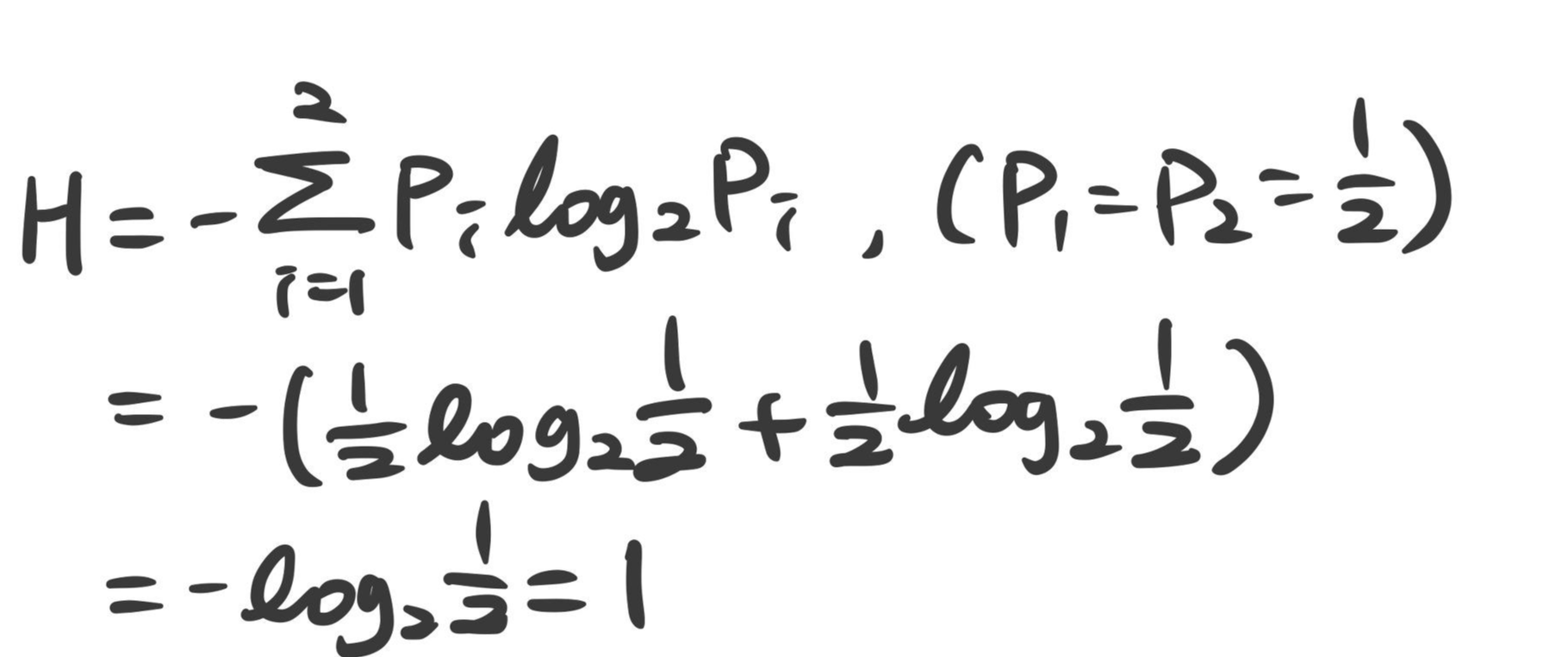
만약 Coin이 Biased Coin일 경우 H와 T의 확률이 같지 않아 엔트로피 값을 통해 예측가능해진다.
<Shannon Entropy의 종류>
① Message Entropy
메시지가 선택됐을 때 얻는 정보의 양
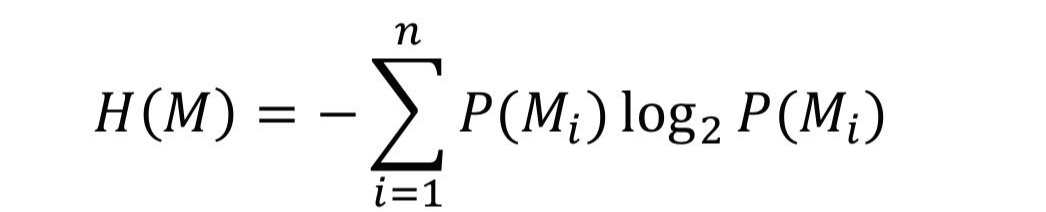
② Key Entropy
Key가 선택됐을 때 얻는 정보의 양
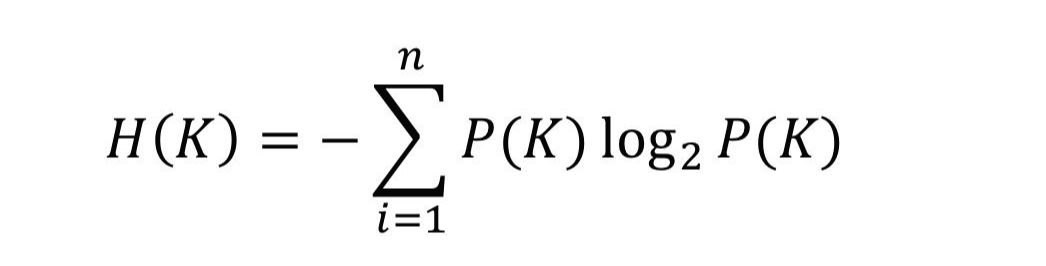
≫ Key Entropy≥Message Entropy일 때 메시지 정보가 완벽히 은폐된다.
Equivocation
equivocation: 모호성
conditional entropies of the key K and message M
앞서 알아본 Entropy 공식에 조건이 추가되었다. ~일 확률이 아닌, ~일때 ~일 확률로 계산한 Entropy이다.
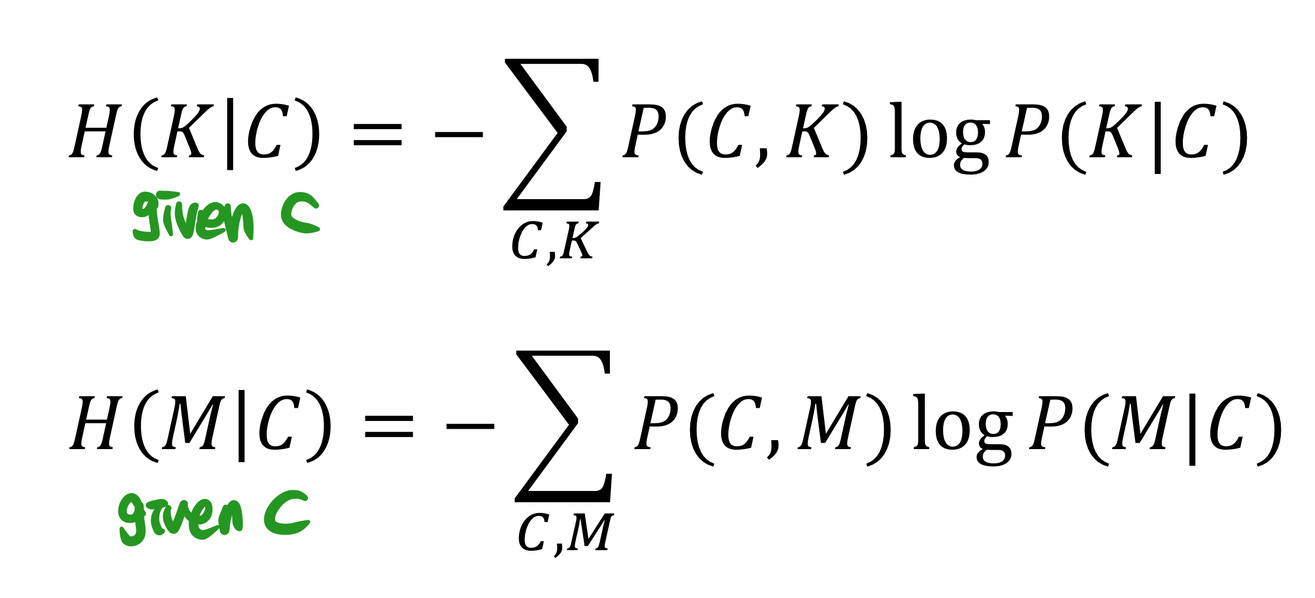
cipher text의 길이가 길수록 uncertainty가 줄어든다. 즉, 예측하기 쉬워진다.
<Perfect Secrecy>
I(M|C) : C가 주어졌을 때 M에 대해 새롭게 알려지는 정보량
I(K|C) : C가 주어졌을 때 K에 대해 새롭게 알려지는 정보량
C가 주어짐으로써 새로 알게된 정보 = Uncertainty - C를 알고 난 뒤의 Uncertainty
I(M|C) = H(M)-H(M|C)
이 때 I(M|C)=0이 되는 것이 가장 이상적이다.
∴H(M)=H(M|C)가 되어야한다.
≫ C가 uncertainty of message를 낮추지 않는다.
또한, H(K)≥H(M)이어야한다. 즉, Key bits 수가 Message bits 수보다 같거나 많아야한다.
유도:
H(M|C)≤ H((M,K)|C) = H(H|C)+H(M|(C,K))
이 때, H(M|(C,K))=0이므로
H(M|C)≤ H(H|C)≤H(K)
H(M|C)=H(M)
∴H(M)≤H(K)
결론 - Perfect secrecy를 위한 조건
① I(M|C)=0, H(M)=H(M|C)
② H(K)≥H(M)
Intercepted Ciphertext
H(M|C1,C2,...,Cn+1)에서 C의 개수가 많아질수록(=정보가 더 많을수록) entropy가 감소한다.
Redundancy
redundancy: 그것이 없어도 본질적인 뜻이 정하지 않는 정보. 즉, 무의미한 정보
D=R-r
R: Absolute Rate of the language, 조합가능한 모든 경우의 bit 수(entropy)
ex) cat, cta, act...
r: Rate of the language, 실제 사용하는 조합의 entropy
ex) cat
R-r의 결과는 사용하지 않는 무의미한 단어가 된다.
Spurious Key Decipherment
spurious: 거짓된
C=E(M,K)이고 C를 생산하는 또 다른 K가 존재할때 spurious key decipherment가 발생한다.
C=E(M,K)=E(M',K')일 때 발생한다.
2H(K)-1개의 spurious key decipherment가 존재한다.
Unicity Distance
무차별 대입 공격에서 가능한 spurious key의 수를 0으로 줄임으로써 암호를 해독하는데 필요한 원래 암호 텍스트의 길이
F:number of false solutions
q:false solution을 생산할 확률
F=(2H(K)-1)q≒2H(K)-DN
log2F=H(K)-DN
Length of Ciphertext가 커질수록 Number of False Solutions이 작아진다.
F 값을 0으로 두어 암호를 해독하는데 필요한 원래 암호 텍스트의 길이를 계산할 수 있다.
0=H(K)-DN
H(K)=DN
N=H(K)/D=Entropy/Redundancy
위 식에서 다음과 같은 관계를 발견할 수 있다.
Entropy↑ : Unicity Distance↑
Redundancy↓ : Unicity Distance↑
Unicity Distance 계산 예

8bits per letter이므로
17.5×8bits=140bit=2blocks
'CS > 정보보안' 카테고리의 다른 글
| 03. Network and Systems (0) | 2021.09.23 |
|---|---|
| 02. History of Cryptography (0) | 2021.09.23 |
| 01. Introduction (0) | 2021.09.11 |

