외판원 문제란?
home city에서 출발해 모든 city를 한번씩 거치고 다시 home city로 돌아오는 최단 경로를 구하는 문제이다.
만약 무식하게 모든 경우의 수를 다 알아본 후 가장 짧은 경로를 찾는다면 그 성능은 어떻게 될까? (n - 1)! 즉 O(n!)이라는 결과가 나온다. 이렇게 비효율적인 방법은 쓸모가 없으므로 우리는 동적계획법을 사용하여 TSP를 풀어보려고 한다.
<shortest path에서 문제에서 사용하는 자료구조>
① W : 그래프의 인접행렬
W[i][j] = 이음선의 가중치 (vi에서 vj로의 이음선이 있는 경우)
= ∞ (vi에서 vj로의 이음선이 없는 경우)
= 0 ( i = j인 경우 )

② V : 모든 정점들이 담긴 집합
③ A : V의 부분집합
④ D[vi][A] : vi에서 A의 집합들을 한번씩 모두 지나면서 v1로 가는 최단경로의 길이
쉽게 이해하면 D[출발 정점][중간에 거치는 애들] 이다.
알고리즘 설계전략
① 재귀 관계식 정립
D[vi][A]값을 계산할 때, vi는 출발점이므로 무조건 지난다고 가정하므로 vi에서 A의 정점들(vi 제외) 중 하나인 vj와의 거리를 W[vi][vj]라고 하고, vj에서부터 1을 찾아가는 것은 이미 계산한 값들이 담긴 D배열로 부터 최단 값을 가져온다. 이 값은 D[vj][A - { vj }]로 표현된다.
D[vi][A] = minimumvj∈A(W[i][j] + D[vj][A - { vj }]) if A≠∅
D[vi][∅] = W[i][1]
② bottom-up 방식으로 해결
처음엔 D배열에 최단값을 미리 저장하고 이를 사용한다는 것이 가능한가 싶기도하고 와닿지않지만, 동적 계획법은 작은 문제에서 큰 문제로 점점 크기를 확장하며 저장한다는 점을 기억하자. 우리는 여기서 A, 즉 D[vi][A] 이 부분에 들어갈 배열의 수가 0개일 때부터 점점 크기를 늘려가며 배열에 저장한다.
이 때, A의 개수가 0개라는 것은 중간에 거치는 곳 없이 바로 v1로 간다는 뜻과 같으므로 D[vi][∅] = W[i][1]이다.
<적용 예>

- A가 0개
D[v2][∅] = 1 (= v2 → v1)
D[v3][∅] = ∞ (= v3 → v1)
D[v4][∅] = 6 (= v4 → v1)
- A가 1개
D[v2][{v3}] = 6 + ∞ = ∞ (= v2 → v3 → v1)
D[v2][{v4}] = 4 + 6 = 10 (= v2 → v4 → v1)
D[v3][{v2}] = 7 + 1 = 8 (= v3 → v2 → v1)
D[v3][{v4}] = 8 + 6 =14 (= v3 → v2 → v1)
D[v4][{v2}] = 3 + 1 = 4 (= v3 → v2 → v1)
D[v4][{v3}] = ∞ + ∞ = ∞ (= v3 → v2 → v1)
이처럼 앞에서 계산해 놓은 값이 뒤에서 다시 사용된다는 것을 확인할 수 있다.
알고리즘 수도코드
※v1,v2,..vj는 각각 v1,v2,..vj를 의미한다. 첨자 표기가 안돼서..
void travel(int n, const number W[], index P[][], number& minlength) {
index i, j, k;
number D[1..n][subset of V-{v1}];
for(i=2; i<=n; i++)
D[i][∅] W[i][1];
for(k=1; k<= n-2; k++)
for(all subsets A⊂V-{v1} containing k vertices)
for(i such that i 1 and vi is not in A) {
D[i][A] = min(W[i][j] + D[j][A-{vj}]);//(j:vj∈A) //basic operation
P[i][A] = value of j that gave the minimum;
}
D[1][V-{v1}] = min(W[1][j]+D[j][V-{v1,vj}]);//2<=j<=n)
P[1][V-{v1}] = value of j that gave the minimum;
minlength = D[1][V-{v1}]
}
알고리즘 분석
basic operation : v1로 가는 최단 길이를 담은 D[i][A] 값을 계산하는 부분(D[i][A] = min(W[i][j] + D[j][A-{vj}]))
basic operation은 3중 포문에 싸여있다. 위에서부터 첫번째 for문은 n-2번, 그 속의 for문은 n-1Ck번(n-1개 중에 k개를 고르므로), 또 그 속의 for문은 n-1-k번 반복하므로 이를 k에 대한 식으로 나타내면 아래와 같다.

위 식에 아래 개념을 적용하여 성능을 알아보자.

- 적용과정 및 결과
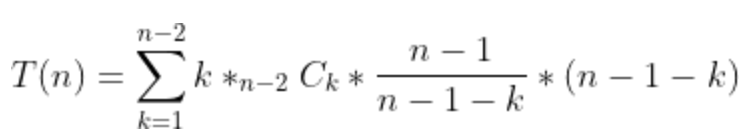

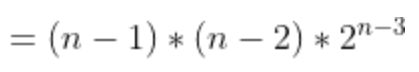
∴Θ(n22n)
'알고리즘 > <3> Dynamic Programming' 카테고리의 다른 글
| [알고리즘] 최적 이진 검색 트리, Optimal Binary Search Trees | 설계 및 분석 (0) | 2021.01.03 |
|---|---|
| [알고리즘] 플로이드 알고리즘, Floyd's Algorithms | 설계 및 분석 , 구현코드 (0) | 2021.01.02 |
| [알고리즘] 이항계수, Binomial Coefficient | 설계 및 분석 (0) | 2021.01.02 |
| [알고리즘] 동적계획법, Dynamic Programming (0) | 2020.12.31 |



